Bio-signal for Emotion Classification

Referred to

• Signal Processing Lecture by Dr. Ajay Kumar Verma 
• 이산 웨이브렛 변환을 이용한 고각성 부정 감성의 GSR 신호 분석(2017, 임현준 외 2)
• https://www.sciencedirect.com/topics/engineering/detail-coefficient
• https://bookdown.org/yuaye_kt/RTIPS/ttest.html

Project Timeline

1번부터 3번까지는 Matlab에 존재하는 신호처리 API를 활용하여 Preprocess

1. Upsampling : Sensor Data와 Emotion Data의 데이터 주기를 맞춥니다. 

2. Nearest Interpolation : 실험에서 데이터가 비어있어 오류가 발생할 수 있는 부분을 보간합니다. 

3. Spline Interpolation : PPG 데이터의 경우 +10000 Outlier가 존재하면 Spline Interpolation 처리를 해줍니다. 이 방식은 인접한 점을 3차 다항식의 값으로 간주하고, 그 사이에 있는 값을 보간합니다. 

 

여기서부터 PPG, GSR, SKT 데이터의 Feature Selection 단계

4. Data Scaling : 세 가지 방법이 있습니다.

     a) Normalization : Normalize하여 0에서 1까지로 표현하도록 합니다. 

     b) Standardization

     c) IQR scaler : 데이터가 심하게 튀어도 결과에 영향이 다른 스케일러보다 크지 않아 Robust 한 특징을 가집니다. 

 

스케일링 단계에서, Raw Data를 스케일링해야 할수도 있고, Feature Extraction 한 후 스케일링이 필요할 수도 있습니다. 또한,데이터를 직접 다뤄보아야 알겠지만, 센서 Raw Data 인 만큼 전압값이 튀는 구간이 심할 때가 있어 자주 쓰이지는 않는 IQR이 필요할 수 있습니다.

 

 

5. Feature Selection : 

PPG 보통 심박변이도(HRV)를 NN간격 혹은 RR간격이라 합니다. Raw Data에 0.3 - 12Hz 4th Order Bandpass Cheby2 Filter를 적용합니다.       시간영역 : NN간격 내 데이터의 최고점과 최저점의 차이      주파수영역 : PSD-저 중 고 영역의 i) Peak   ii) Area   iii) Percentage

GSR 우선, 1Hz 4차 Butterworth Filter 적용합니다. 신호를 Tonic 성분 (필요없는 배경신호), Phasic 성분(감정변화와 관련있는 성분)으로 분해 후 Phasic 성분의 4가지 특징을 추출해야 합니다.   영교차율=분석구간 내 신호 파형이 영점축과 교차하는 횟수. 높은 흥분 상태일수록 신호의 진동이 강해지고 높은 영교차율을 갖습니다.  SCVSR=Skin Conductance Very Slow Response  SCSR=Skin Conductance Slow Response      시간영역 : 급격한 하강점      주파수영역 : Wavelet Transform(dB3, Level 10)            Phasic 성분의 최댓값           Phasic 성분의 진폭            SCVSR 신호의 영교차율            SCSR 신호의 영교차율 주파수 영역에서 특징을 추출하기 위한 방법은 다음과 같습니다.  1) 움직임으로 인한 잡음, 직류성분 제거를 위해 IIR 구조의 1Hz 4차 버터워스 구조를 가진 저역 통과 필터 적용  2) Discrete Wavelet Transform으로 Tonic, Phasic으로 분해. Wavelet은 Daubechies (db3)를 활용합니다.     SCVSR = 0 - 0.08[Hz]      SCSR = 0 - 0.2[Hz] 대역의 신호를 추출해냅니다.  선행 연구에서는 32GHz GSR 신호를 Level 10 Decomposition 을 통해 원하는 Tonic 대역폭에 해당하는 신호를 구할 수 있었고, Phasic=Signal-Tonic 의 간단한 수식을 이용하였습니다.  이산 웨이브렛 변환을 이용한 고각성 부정 감성의 GSR 신호 분석(2017, 임현준 외 2)   Sliding Window 방식과 아래 수식을 이용하여 Phasic의 최댓값과 진폭을 구합니다. 두 값은 보통 감정의 긴장 수준과 비례하여 커지는 경향을 보입니다.

SKT 시간영역 : i) Mean  ii) Std(Standard Deviation)  iii) Max(Max Value of Amplitude)

 

6. Scatter Plot : Plotting 후 분포/추이를 확인합니다. 

7. Anova / T-Test : 유의미한 차이여도 수치상으로 차이가 나지 않으면 학습시켜도 의미가 없을 수 있습니다. 이러한 여부를 Anova / T-Test 두 방법으로 검토합니다. 구간학습시키는 의미가 없는 데이터는 

8. 유의미한 변수 추출

9. 감정 Labelling : Valence - Arousal 사분면을 정하고, High, Low의 기준을 정해 [Valence, Arousal] 형식으로 표현할 수 있도록 합니다.

 

여기서부터 Machine Learning Algorithm을 준비하고 적용합니다.

10. 머신러닝 모델 선정

PNN, SVM, Random Forest, k-NN

 

 

---

Wavelet Transform / Filter 

웨이브렛의 적용분야는 Compression, Denoising, Discontinuity Detection, Audio Enhancement & Effects, Image Fusion 등이 있습니다. 사용 라이브러리는 Python High Level Interface로 만들어져있지만, 추상화 레이어 아래에서는 C가 동작하고 있습니다. 

Wavelets with filters			Wavelets without filters
With compact support		With non-compact  support	Real	Complex
Orthogonal	Biorthogonal	Orthogonal	gaus, mexh, morl	cgau, shan, fbsp, cmor
db, haar, sym, coif	bior	meyr, dmey, btlm

필터가 있는 웨이브렛만 Filter Bank를 적용할 수 있습니다. 

 

API Usage

dwt() : Single-Level Discrete Wavelet Transform

idwt() : Single-Level Discrete Inverse Transform 

 

haar wavelet 이 사용된 예시

import pywt 
x = [3, 7, 1, 1, -2, 5, 4, 6] 

#cA : contains approximation coefficients 
#cD : contains detailed coefficients
cA, cD = pywt.dwt(x, 'haar')
y = pywt.idwt(cA, cD, 'haar')

print(cA)
print(cD)
print(y)

 

wavedec(x, 'wavelet', mode='sym', level=n) : Multi-Level Discrete Wavelet Transform

waverec(coeffs, 'wavelet', mode='sym') : Multi-Level Discrete Inverse Transform 

import pywt 

x = [3, 7, 1, 1, -2, 5, 4, 6, 6, 4, 5, -2, 1, 1, 7, 3] 

coeffs = pywt.wavedec(x, 'db1', level=2, mode='periodic')
cA2, cD2, cD1 = coeffs
y = pywt.waverec(coeffs, 'db1', mode = 'periodic')

print('cA2=', cA2)
print('cD2=', cD2)
print('cD1=', cD1)
print('Reconstructed Signal = ", y)

wavedec 함수의 경우 리턴값은 [cA_n, cD_n, cD_n-1, ... , cD2, cD1] 리스트 형태로 나타납니다. 

 

Denoising using Wavelet Transform 

f(k) -> DWT(Analysis or Decomposition) -> Thresholding(Estimate noise level and set thresholds) -> IDWT(Synthesis or Reconstruction) -> f'(k) 

y = denoise_wavelet(x, wavelet='db1', mode='soft', wavelet_level=n, method='BayesShrink', rescale_sigma='True') 

import numpy as np
import pywt
from skimage.restoration import denoise_wavelet 
import matplotlib.pyplot as plt 

#bring library's internal sample datasource 
x = pywt.data.ecg().astype(float)/256

sigma = 0.05
x_noisy = x + sigma * np.random.randn(x.size)

#wavelet denoising 
x_denoise = denoise_wavelet(x_noisy, method='BayesShrink', mode='soft', 
                            wavelet_levels=3, wavelet='sym8', rescale_sigma='True')

plt.figure(figsize=(20, 10), dpi=100)
plt.plot(x_noisy)
plt.plot(x_denoise)

 

 

코드로직 설계 : GSR Data 

Valence 와 Arousal 데이터와 대조하며 의미있어 보이는 GSR 데이터를 30초 길이가 되게끔 자른 후 시간 영역과 주파수 영역에서의 데이터 처리를 적용합니다. 

주파수 영역에서는 Wavelet Transform을 적용합니다. 

논문中 : GSR신호에서 Tonic 성분을 빼줌으로서 Phasic 성분을 계산 ... Phasic 성분의 SCVSR(0-0.08Hz) 는 A8에서 A10을 빼줌으로서 근사적으로 0.016-0.06 Hz로 구성. SCSR신호 (0-0.2 Hz)는 A6에 A10을 빼줌으로 근사적으로 0.016 - 0.25Hz로 구성

Phasic = GSR - Tonic

 

시간영역 

급격한 하강점은 미분값으로 찾습니다. 

 

주파수영역 

1. 데이터 파일입력 

2. Mother Wavelet 정의 

3. Decomposition Level 정의 : Level 6, Level 8, Level 10 (A10은 Tonic 성분에 해당) 

4. 각 성분 구하기 

Phasic 성분 = Raw Signal - Tonic 성분 (A10) 

Sliding Window 방식으로 Phasic 성분의 최댓값, 진폭 구하기  최댓값과 진폭은 불쾌, 불안감과 상관관계 있음

SCVSR(Skin Conductance Very Slow Response) = A8 - A10  SCSR(Skin Conductance Slow Response) = A6 - A10  0-1 크기로 정규화 처리, 정규화된 신호의 중간값(Median)을 문턱값으로 지정 영교차율 구하기

ScienceDirect의 Detail Coefficient 칼럼에서는 다음과 같이 Denoising 방법을 설명합니다.

아래 그래프에서는 노이즈가 없는 파형과 노이즈가 추가된 파형을 Wavelet Decomposition 8단계까지 거칠 시 나오는 모든 Detail Coefficient를 나타내었습니다. 매끄러운 시그널을 만들기 위해서 특정 coefficient를 0으로 만들거나 변형시켜주어 다시 Reconstruction 시키는 것입니다. 

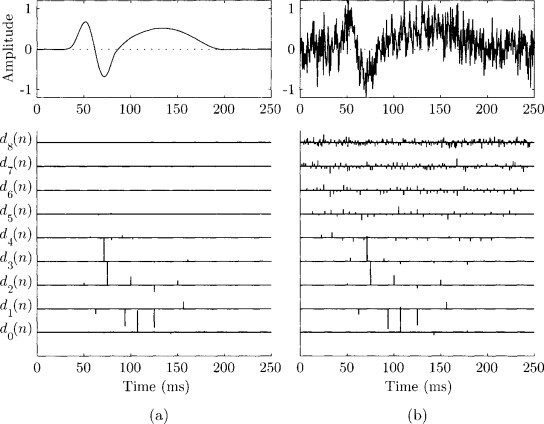
위에서 보이는 것처럼 노이즈에 해당하는 coefficient는 scale이 높을 때 더 많이 나타납니다. 따라서, 통상적으로 0으로 만들어주는 Coefficient는 j 가 J_T 보다 큰 것들입니다. 

where J = finest scale in wavelet decomposition

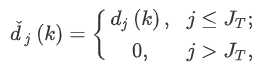
Subject 2의 Wavelet Decomposition 후 나오는 Coefficient 들은 다음과 같습니다. 편의상 D10 - D4 까지만 나타내었습니다. 

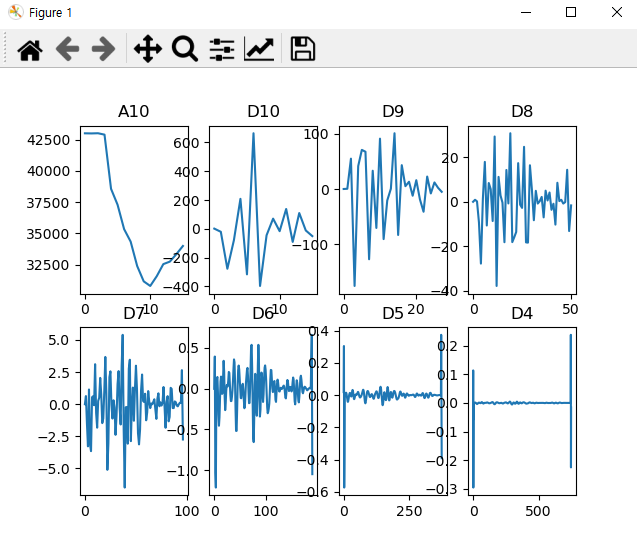
'db3'를 활용한 Wavelet Decomposition 을 거친 결과이며, A10의 요소만을 남겨두기 위해서는 나머지 Detailed Coefficient를 모두 0으로 만들어주는 절차를 거쳐야 합니다. 따라서, 절차는 다음과 같아집니다.

1. Level n Wavelet Decomposition (wavedec function)

2. Remove all Detailed Coefficients from Dn to D1 

3. Wavelet Reconstruction (waverec function) 

 

Subject 2의 Decomposition Tree의 Level을 10까지, Detailed Coefficient를 Zero-out 하고 복원했을 때는 다음과 같은 결과를 보입니다. 파형에 존재하던 디테일이 조금 사라져 매끄러워진 것을 볼 수 있습니다. 

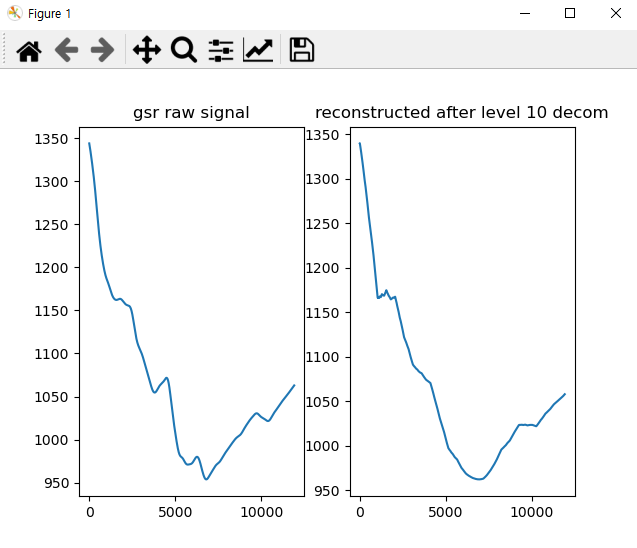
이와 같은 방법으로 Raw GSR Signal에서 A10 Reconstructed(after detail coefficients zeroed out) 를 빼주어 Phasic을 구하면 다음과 같은 결과를 얻게 됩니다.

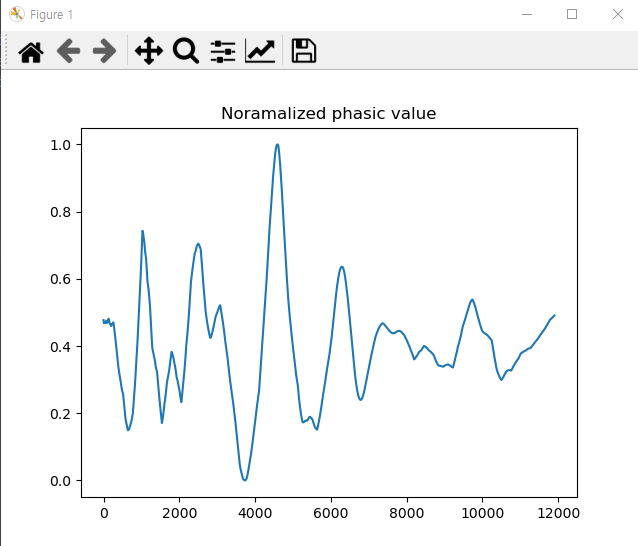
여기서 정규화를 위한 function call은 다음과 같았습니다. 

# 정규화 (Min-Max Scale Normalization) 

from sklearn.preprocessing import minmax_scale

minmax_scale(array)

 

이후 영교차율을 구합니다. 로직은 다음과 같이 작성합니다. 

# Zero Crossing (영교차율 구하기) 

zero_cross = np.nonzero(np.diff(array > 0))[0]