PyTorch Basics(1)
Referred to : Prof. Sung Kim's PyTorch Lecture
Linear Model


y_hat 은 forward function 에 정의되어 있으며 예측값을 나타냅니다. loss는 예측값에서 실제 값을 빼고 제곱한 값을 나타냅니다. 데이터 셋에서 나온 loss 값의 평균을 취해주면 Mean Squared Error (MSE)를 얻을 수 있습니다.
import torch
import numpy as np
import matplotlib.pyplot as plt
w = 1.0
def forward(x):
return x * w
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) * (y_pred - y)
x_data = {1, 2, 3}
y_data = {2, 4, 6}
w_list = []
mse_list = []
for w in np.arange(0.0, 4.1, 0.1):
print("w=", w)
l_sum = 0
for x_val, y_val in zip(x_data, y_data):
y_pred_val = forward(x_val)
l = loss(x_val, y_val)
l_sum += l
print("\t", x_val, y_val, y_pred_val, 1)
print("MSE=", l_sum / 3)
w_list.append(w)
mse_list.append(l_sum / 3)
plt.plot(w_list, mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()
Gradient Descent Algorithm
loss를 최소화하는 w를 찾는 과정에서, Training Data가 많다면 w를 일일이 확인할 순 없고, 자동으로 찾아내는 방법이 필요할 것입니다. 이것을 구하는 알고리즘이 Gradient Descent 알고리즘입니다. 찾고자 하는 구간은 loss 그래프에서 gradient 가 minimum이 되는 구간입니다.

import torch
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = 1.0
# linear
def forward(x):
return x * w
def loss (x, y):
y_pred = forward(x)
return (y_pred - y) * (y_pred - y)
# d_loss / d_w
def gradient(x, y):
return 2 * x * (x * w - y)
# Before Training
print("predict (before training)", 4, forward(4))
# Training loop
for epoch in range(100):
for x_val, y_val in zip(x_data, y_data):
grad = gradient(x_val, y_val)
w = w - 0.01 * grad
print("\tgrad: ", x_val, y_val, grad)
l = loss(x_val, y_val)
print("progress:", epoch, 'w=', w, 'loss=', l)나타나는 결과는 다음과 같습니다. loss 만 표기합니다.
progress: 0 w= 1.260688 loss= 4.919240100095999
progress: 1 w= 1.453417766656 loss= 2.688769240265834
progress: 2 w= 1.5959051959019805 loss= 1.4696334962911515
...
progress: 99 w= 1.9999999999999236 loss= 5.250973729513143e-26
weight 값을 두 개 갖는 경우를 생각해볼 수 있습니다.

각각의 weight를 Partial Differential로 계산해준 후 gradient를 따로 계산합니다. b 값은 직접 조금씩 바꿔가며 계산하였고, weight를 gradient descent 로 알아서 수정하게끔 하였습니다.
import torch
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w1 = 1.0
w2 = 1.0
b = 10.0
# linear
def forward(x):
return x*x*w2 + x*w1 + b
def loss (x, y):
y_pred = forward(x)
return (y_pred - y) * (y_pred - y)
# d_loss / d_w
def gradient_w1(x, y):
return 2*x*((x*x)*w2 + x*w1 + b - y)
def gradient_w2(x, y):
return 2*x*x*(x*x*w2 + x*w1 + b - y)
# Before Training
print("predict (before training)", 4, forward(4))
# Training loop
for epoch in range(100):
for x_val, y_val in zip(x_data, y_data):
grad1 = gradient_w1(x_val, y_val)
grad2 = gradient_w2(x_val, y_val)
w1 = w1 - 0.01 * grad1
w2 = w2 - 0.01 * grad2
print("\tgrad1: ", x_val, y_val, grad1)
print("\tgrad2: ", x_val, y_val, grad2)
l = loss(x_val, y_val)
print("progress:", epoch, 'w1=', w1, 'w2=', w2, 'loss=', l)progress: 0 w1= 0.09632000000000007 w2= -0.8790399999999998 loss= 13.121781759999987
...
progress: 99 w1= -6.93641650142263 w2= 1.8725996890776992 loss= 0.0019490191884949431
b(model equation's constant)를 10.0 첫 w1과 w2 각각 1.0으로 설정해주고 epoch 100번을 돌렸을 때, Training 된 w1은 -6.93, w2는 1.87이 나옵니다. 이는 b를 변경하였을 시 바뀔 수 있습니다. b를 3.0으로 설정하면 loss 가 조금 개선된 것을 볼 수 있습니다.
progress: 99 w1= -0.8292703583553376 w2= 0.605378183969827 loss= 0.0015529446988470663
Back Propagation
지금까지는 간단한 linear model 에서의 gradient를 구하고, gradient descent를 적용하여 최적의 weight를 찾아내게끔 하였습니다. 그러나 Network가 복잡해지고 노드간 비선형적 관계와 같은 요인 때문에 일일이 loss와 d(loss)/d(w)를 계산하기가 힘들어집니다. 이러한 경우에는 computational graph를 만들고 chain rule 을 이용하여 구한 각각의 gradient를 곱해 최종 gradient를 구할 수 있습니다. 이를 Back Propagation 이라고 합니다. Chain rule의 기본 개념은 다음과 같습니다.

노드가 많아질수록 적용되어야 하는 chain rule 의 길이도 늘어납니다. 이를 간단한게 계산하는 방법은 각 요소를 먼저 계산하고 나중에 곱해주는 것입니다. 이전에 사용한 모델에 back propagation을 적용시켜보겠습니다.

우선 위 식에 대한 computational graph를 만듭니다. 첫 단계는 forward pass 를 계산하는 것으로, graph에서 요구하는 계산을 하면 됩니다. 이후 단계를 들어가기 전에, Input, Output 관계에 대해 각 단계에서 수식을 유도해나가야 합니다 (초록, 보라, 주황). 보라색을 예로 들면,
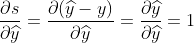
처럼 유도가 됩니다. 유도되는 관계식은 수학적 모델이 바뀌지 않는 이상 변화하지 않으며, 초기 변수를 바꾸어도 같아야 할 것입니다.

PyTorch를 사용하면 computational graph 를 일일이 만들어 줄 필요 없이 자동으로 생성하게끔 할 수 있습니다.
import torch
from torch.autograd import Variable
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = Variable(torch.Tensor([1.0]), requires_grad=True)
def forward(x):
return x * w
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) * (y_pred - y)
# Before Training
print("predict (before training", 4, forward(4).data[0])
# Training loop
for epoch in range(10):
for x_val, y_val in zip(x_data, y_data):
l = loss(x_val, y_val)
l.backward()
print("\tgrad: ", x_val, y_val, w.grad.data[0])
w.data = w.data - 0.01 * w.grad.data
# Manually zero the gradients after updating weights
w.grad.data.zero_()
print("progress:", epoch, l.data[0])
#After Training
print("predict (after training)", 4, forward(4).data[0])predict (before training 4 tensor(4.)
grad: 1.0 2.0 tensor(-2.)
grad: 2.0 4.0 tensor(-7.8400)
grad: 3.0 6.0 tensor(-16.2288)
...
predict (after training) 4 tensor(7.8049)